K-Means Clustering

K-Means Clustering은 백오피스(Back Office)에서 자주 활용되는 기법이다.
예를 들어, 비슷한 특성을 가진 고객 데이터를 그룹화할 때 효과적으로 사용할 수 있다.
K-Means Clustering은 데이터를 K개의 그룹(클러스터)으로 자동 분류하는 비지도 학습 알고리즘으로, 각 데이터 포인트를 가장 가까운 중심점에 할당하고,
그룹의 중심점을 반복적으로 업데이트하여 최적의 클러스터를 형성한다. 주로 고객 세분화, 이미지 압축, 이상 탐지 등에 활용되며,
최적의 K값은 엘보우 메서드(Elbow Method)를 통해 결정한다.
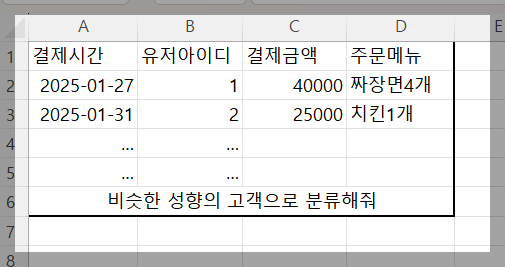
이 데이터에서는 고객을 분류할 정답(Y 값)이 없기 때문에 지도 학습(Supervised Learning) 방식으로 학습할 수 없다.
지도 학습은 입력(X)과 정답(Y)이 있어야 하지만, 여기서는 정답이 없기 때문에 적용이 불가능하다.
대신, 비슷한 성향의 고객을 자동으로 그룹화하는 비지도 학습(Unsupervised Learning)을 사용해야 한다.
이러한 경우 K-Means Clustering 같은 알고리즘을 활용하여 비슷한 고객끼리 묶을 수 있다.

비슷한 성향의 고객을 묶어야 예를 들면 맞춤형 쿠폰을 발송과 같은 방법을 이용하여 지출을 유도할 수 있다.
하지만 현재 데이터에는 고객을 분류할 정답(Y 값)이 없기 때문에 지도 학습(Supervised Learning)을 적용할 수 없다.
즉, Y 값이 없으므로 학습할 트레이닝 데이터도 필요 없으며, 지도 학습 방식이 아니라 비지도 학습(Unsupervised Learning) 방법을 사용해야 한다.





데이터를 효과적으로 그룹핑(클러스터링)하기 위해, 1부터 10개의 그룹(클러스터)을 만들어보고 비교하여 최적의 그룹 개수를 찾는 과정을 수행해보겠다.
1. 그룹의 개수를 어떻게 결정하는가?
데이터를 보면, 우리는 자연스럽게 거리를 고려하여 비슷한 데이터끼리 묶는 것이 더 적절하다는 것을 직관적으로 알 수 있다. 즉, 우리도 모르게 거리 기반으로 데이터를 분류하는 과정을 수행하는 것이다.
예를 들어, 하나의 그룹으로 모든 데이터를 묶으면 너무 광범위해서 이상함을 느끼게 된다. 반대로, 비슷한 데이터끼리 묶으면 논리적으로 적절하게 보인다. 이러한 방식으로 컴퓨터도 거리를 계산하여 가장 적절한 방식으로 데이터를 그룹핑한다.
2. 컴퓨터는 어떻게 그룹을 나누는가?
컴퓨터는 각 데이터와 중심점(centroid) 사이의 거리를 계산하여 가장 가까운 중심점에 데이터를 배정하는 방식을 사용한다.
즉, 다음과 같은 과정이 반복된다.
- 초기에 임의의 중심점을 설정한다.
- 각 데이터가 가장 가까운 중심점에 배정된다.
- 그룹의 중심을 다시 계산하여 업데이트한다.
- 이 과정을 반복하면서 그룹이 점점 최적화된다.
이때, 그룹이 적절하게 형성되었는지 판단하는 기준이 필요하며, 각 데이터가 속한 중심점과의 거리 합을 계산하는 방식을 사용한다. 이 거리의 합이 작을수록 잘 그룹핑된 것으로 간주한다.


3. 그룹 개수를 어떻게 최적화하는가?
그룹의 개수가 많아질수록 데이터는 더 세분화되지만, 일정 개수 이상이 되면 성능 향상이 미미해진다.
이를 확인하기 위해, 각 그룹의 중심으로부터 데이터 간 거리 제곱합(WCSS, Within-Cluster Sum of Squares)을 계산한다.
- 그룹을 1개로 설정하면 WCSS 값이 크다.
- 그룹을 2개로 나누면 WCSS 값이 크게 줄어든다.
- 3개, 4개로 나눌수록 WCSS 값은 줄어들지만, 어느 순간부터 줄어드는 폭이 작아진다.
이러한 변화를 그래프로 나타내면, 처음에는 급격히 감소하다가 어느 순간부터 완만하게 줄어드는 지점이 존재하는데, 이를 최적의 그룹 개수로 설정한다. 이 방법을 엘보우 메서드(Elbow Method)라고 한다.
즉, 그래프의 꺾이는 지점(팔꿈치 모양처럼 보이는 지점)이 가장 적절한 클러스터 개수가 되는 것이다. 너무 많은 그룹을 설정하면 의미가 퇴색되므로, 적절한 그룹 개수를 찾는 것이 중요하다.
Hierarchical Clustering

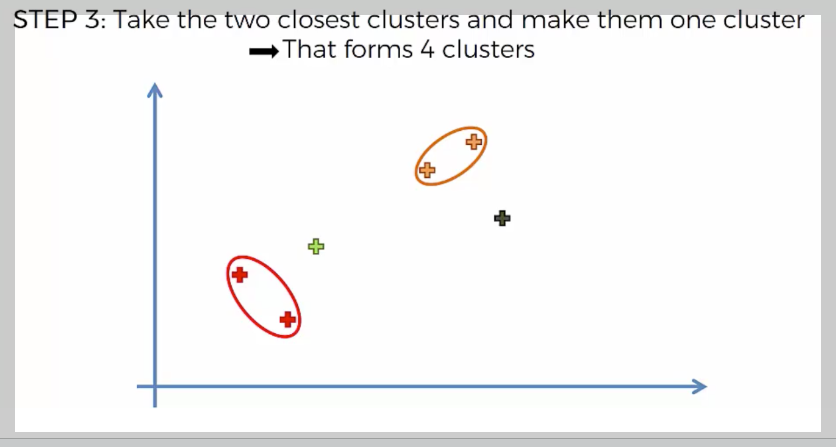
Hierarchical Clustering(계층적 군집화)은 중심점을 잡고 평균을 내는 방식이 아니라, 모든 데이터 간 거리를 계산하여 가장 가까운 것부터 순차적으로 묶는 방식이다.
우리가 보기에는 특정 그룹으로 묶으면 좋아 보일 수 있지만, 컴퓨터는 눈이 없기 때문에 모든 데이터 간의 거리를 계산하고, 가장 가까운 것들부터 묶어 나가는 방식을 사용한다.
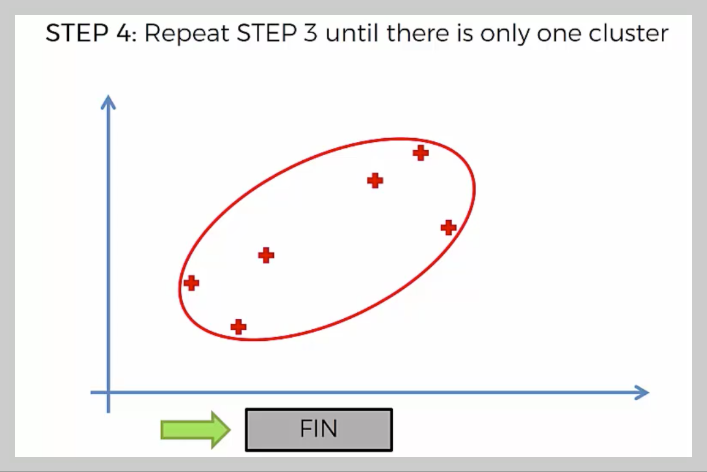
이렇게 거리가 가장 가까운 데이터들을 계속 묶어 나가면서 계층적 구조를 형성하며, 최종적으로 모든 데이터가 하나의 클러스터가 될 때까지 병합을 반복한다.
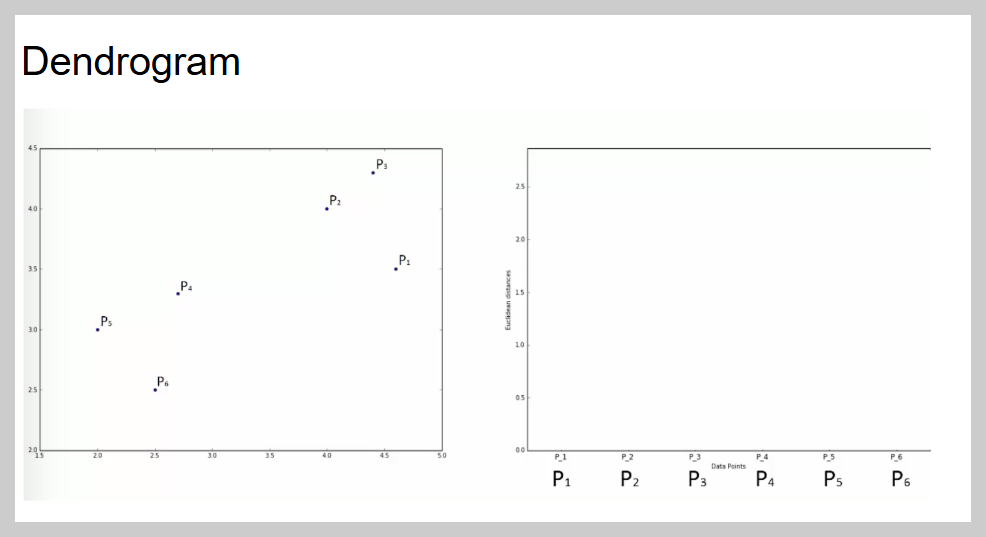
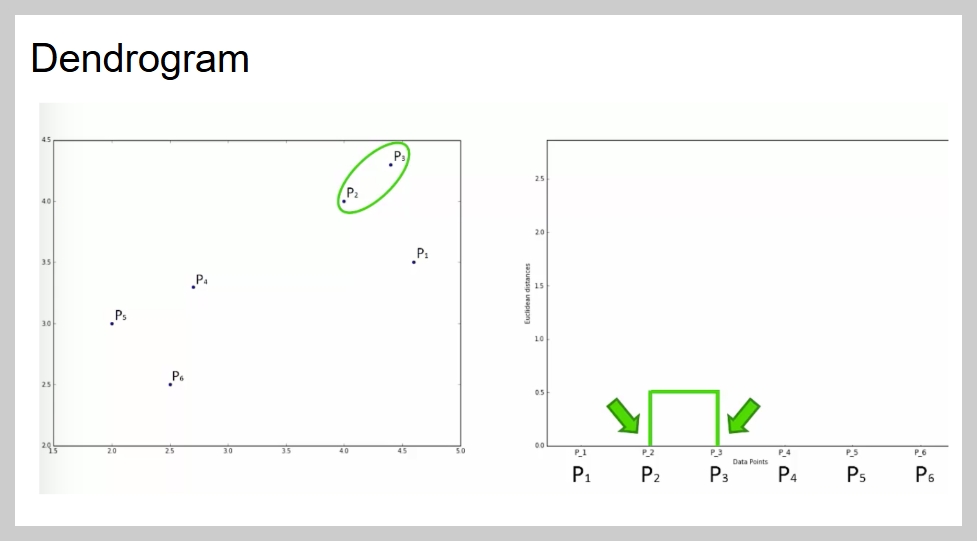
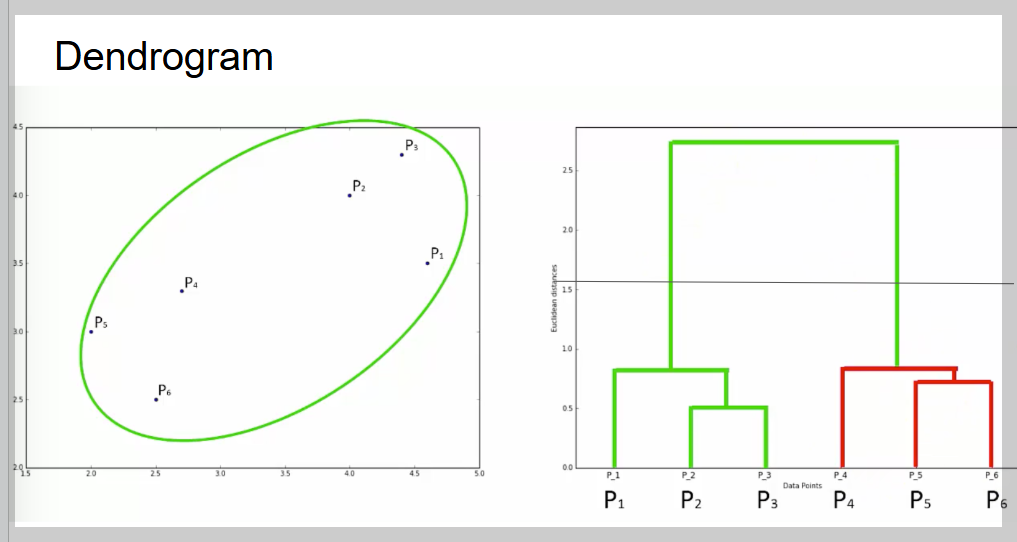
Hierarchical Clustering(계층적 군집화)은 데이터를 거리가 가까운 순서대로 묶어 나가면서 하나의 큰 그룹이 될 때까지 병합하는 방법이다.
이 과정을 덴드로그램(Dendrogram)이라는 그래프로 표현하며, X축은 데이터, Y축은 거리(유사도)를 나타낸다. 그룹을 결정할 때는 덴드로그램에서 긴 선을 찾아 가로로 잘라서 그룹 개수를 정한다.
K-Means vs. Hierarchical Clustering 차이
- K-Means는 WCSS 값을 보고 최적의 클러스터 개수를 정함.
- Hierarchical Clustering은 덴드로그램을 보고 적절한 그룹 개수를 판단함.
즉, K-Means는 수치적 계산을 기반으로, 계층적 군집화는 시각적 판단을 활용하는 방식이다.
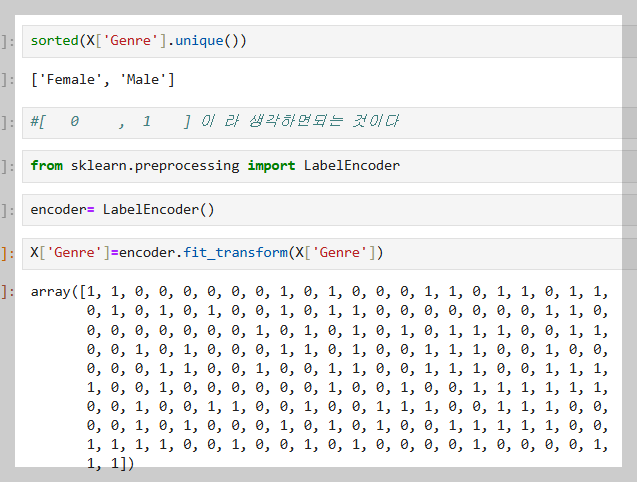
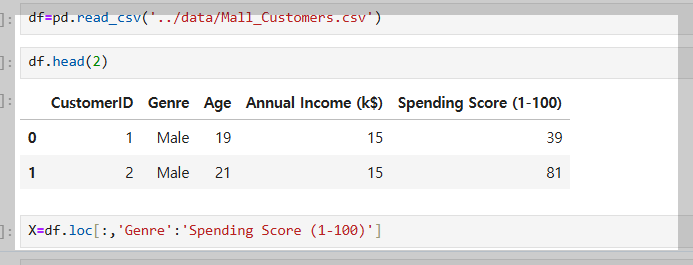
데이터 가공화를 먼저 해준다.
import scipy.cluster.hierarchy as sch
sch.dendrogram(sch.linkage(X,method='ward'))
plt.show()
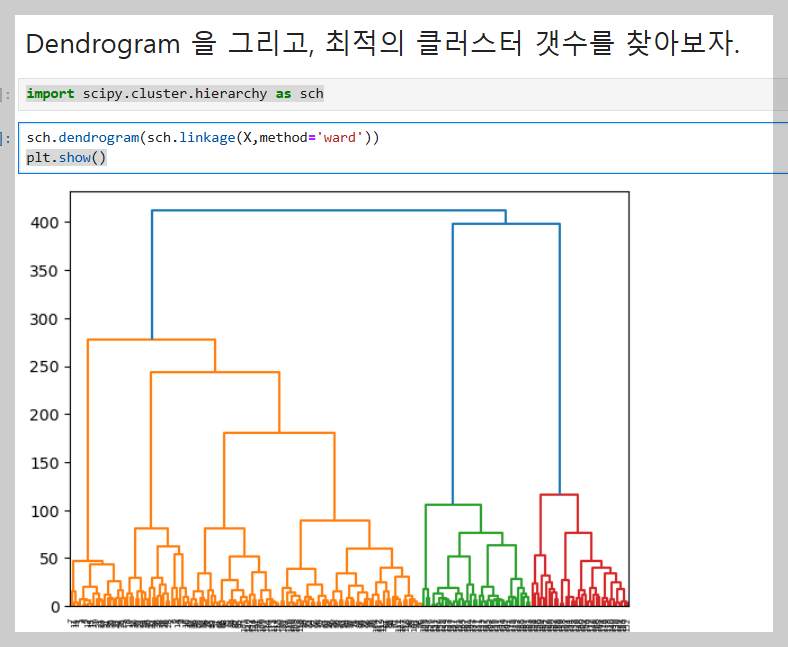
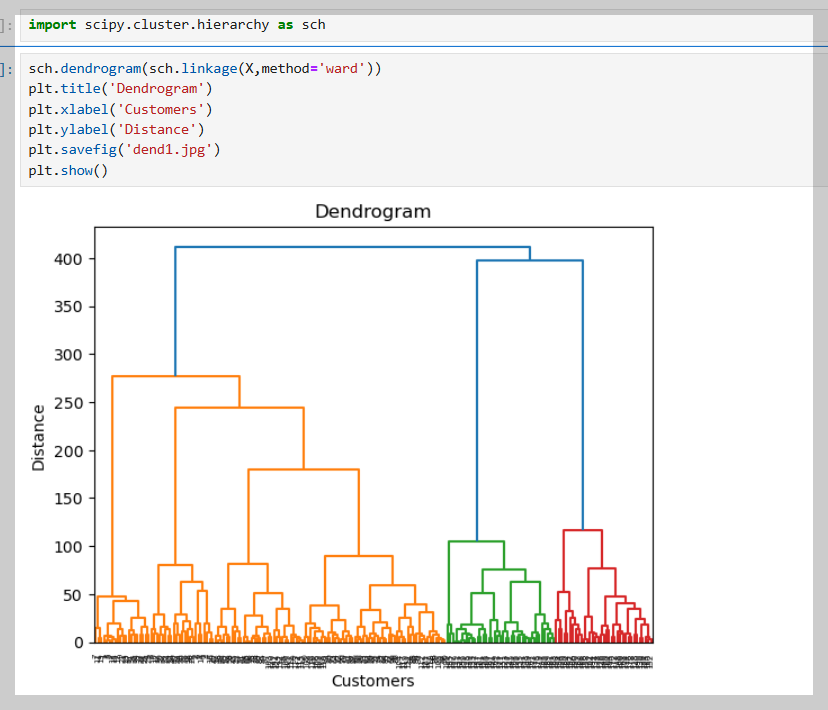
이 이미지는 덴드로그램(Dendrogram)을 이용해 최적의 클러스터 개수를 찾는 과정을 보여준다.
- 왼쪽: 덴드로그램을 그리는 코드 (scipy.cluster.hierarchy 사용).
- 가운데: X축(고객 데이터), Y축(거리)을 나타내며, 가까운 데이터끼리 묶인다.
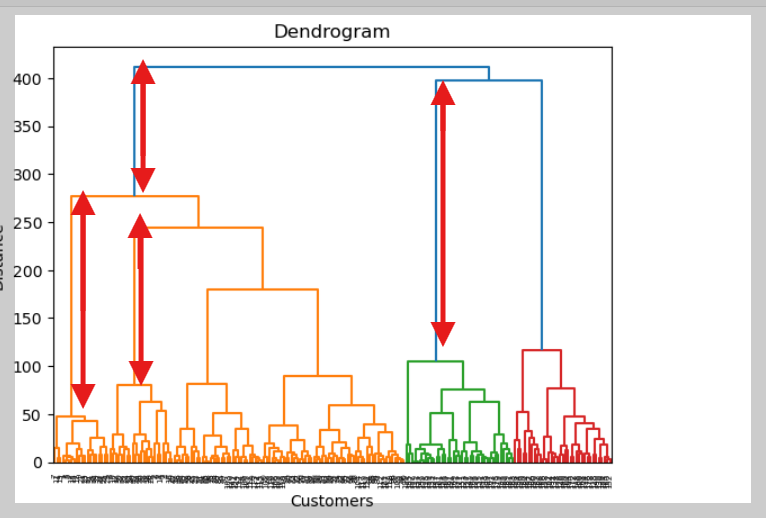
- 오른쪽: 빨간 화살표는 데이터 병합 과정, 긴 선을 기준으로 가로선을 그어 클러스터 개수를 결정.
➡ 결과적으로 클러스터 개수를 6개로 설정하면 적절한 그룹을 만들 수 있다.
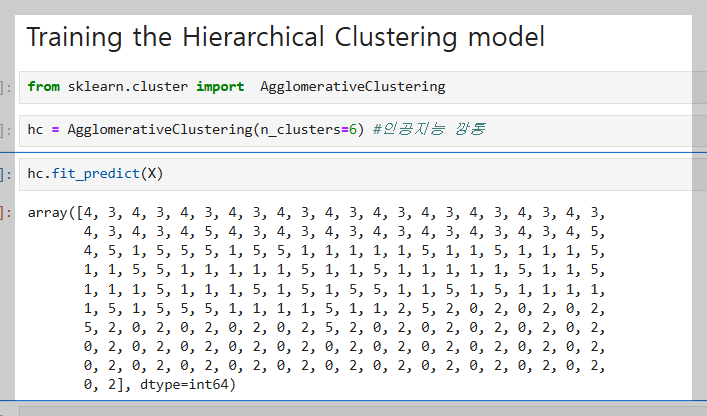
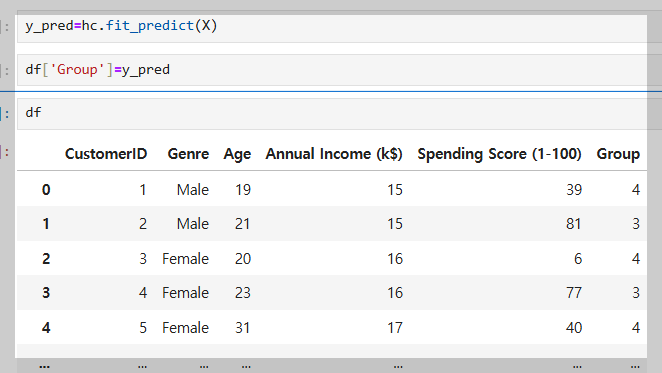
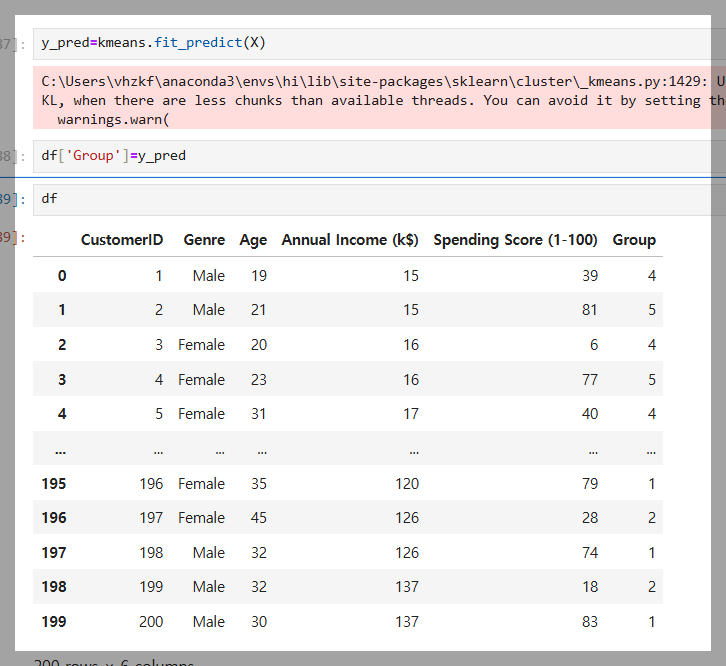
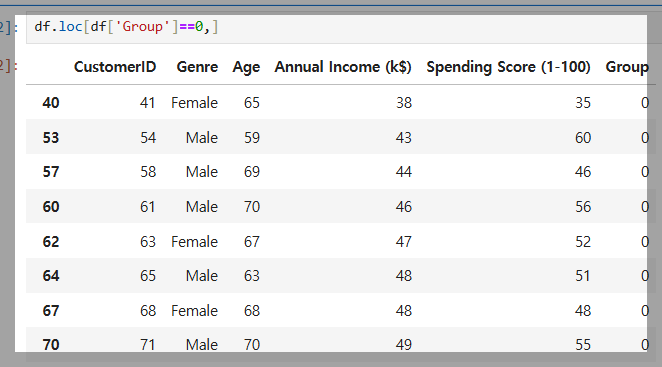
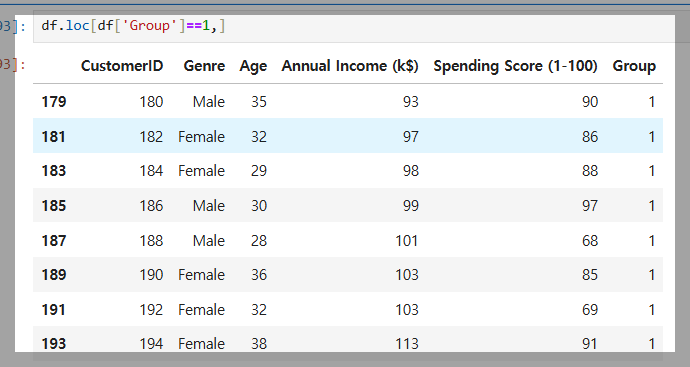
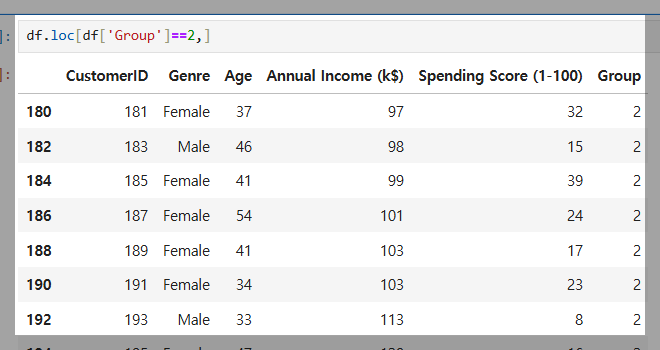
계층적 군집화(Hierarchical Clustering)를 사용해 고객 데이터를 그룹으로 분류한 결과이다.
fit_predict(X)로 각 고객의 그룹을 예측하고, 데이터프레임(df)에 추가하여 비슷한 성향의 고객을 그룹화했다.
'Python > 실습' 카테고리의 다른 글
| 파이썬 : Decision Tree (0) | 2025.01.31 |
|---|---|
| 서포트 벡터 머신(SVM) 실습: 분류와 정확도 분석 (0) | 2025.01.31 |
| 파이썬 : K-Nearest Neighbor (0) | 2025.01.29 |
| 파이썬: 수익 예측 인공지능 만들기 (1) | 2025.01.27 |
| 경력과 연봉 관계 분석 하는 인공지능 만들기 (0) | 2025.01.24 |